What are the key learning points about the features of waves?
Definitions of the features of a wave.
How to calculate amplitudeThe amplitude of a wave is its maximum displacement from its undisturbed position., frequencyThe number of waves produced each second. The unit of frequency is hertz (Hz)., period (wave)The time taken for one complete wave to pass a point or the time for one complete oscillation or vibration. and wave speed.
What are the main features of a wave?
What is amplitude?
As waves travel, they set up patterns of disturbance.
The amplitude of a wave is its maximum displacement from its undisturbed position.
Key fact
It is important to note that the amplitude is not the distance between the top and bottom of a wave
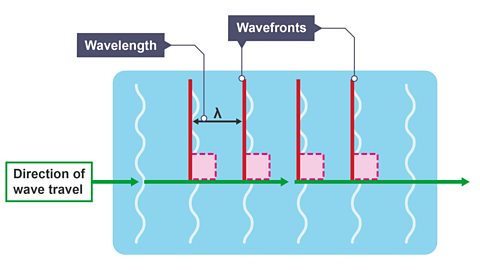
What is wavelength λ?
The wavelength of a wave is the distance between a point on one wave and the same point on the next wave.
It is often easiest to measure this from the troughThe bottommost point of a wave. of one wave to the trough of the next wave, or from the crestThe topmost part of a wave. of one wave to the crest of the next wave.
But it doesn't matter where you measure it - as long as it is the same point on each wave.
The symbol for wavelength is the Greek letter lambda, λ.
What is frequency f?
The frequency of a wave is the number of waves produced by a source each second.
It is also the number of waves that pass a certain point each second.
The unit of frequency is the hertz (Hz).
It is common for kilohertz (kHz), megahertz (MHz) and gigahertz (GHz) to be used when waves have very high frequencies.
For example:
Most people cannot hear a high-pitched sound above 20 kHz, (20 000 Hz).
Radio stations broadcast radio waves with frequencies of about 100 MHz, (100 000 000 Hz).
Most wireless computer networks operate at 2.4 GHz.
Remember:
kilo (thousand) k = 1x103 (1 000)
mega (million) M = 1x106 (1 000 000)
giga (billion) G = 1x109 (1 000 000 000).
The frequency of a wave can be calculated using the equation:
\(\text{frequency f =}~\frac{\text{number of waves to pass a point}}{\text{time taken in seconds}}\)
How are waves measured?
What is period T?
The period of a wave is the time taken for one complete wave to pass a point or the time for one complete oscillationsThe repeated and regular fluctuations, above and below the same position, eg the pressure of a sound wave or the voltage of an alternating current. or vibration.
Period is measured in seconds.
What are wavefronts?
This is an imaginary surface that we draw to represent the vibrating part of a wave.
If you draw semi-circular sound waves spreading out from a speaker, the semi-circular lines are the wavefronts.
The distance between two wavefronts is one wavelength, λ.
What is the wave speed equation?
The speed of a wave is related to its frequencyThe number of waves produced each second. The unit of frequency is hertz (Hz). and wavelengthThe length of a single wave, measured from one wave peak to the next., according to the equation:
\(wave~speed~(v) = frequency (f) \times wavelength (\lambda)\)
\(v = f~ \lambda\)
where:
v = wave speed in metres per second, m/s
f = frequency in hertz, Hz
\(\lambda\)(lambda) = wavelength in metres, m
All waves, including sound waves and electromagnetic waves, follow this equation.
It should be noted that some particular waves have their own specific speeds:
The speed of light and all of the electromagnetic spectrum in a vacuum is 300,000,000 m/s or 3×108 m/s.
The speed of sound in air is often taken to be 340 m/s, but this can vary depending on temperature and pressure.
Question
What is the speed of a water wave that has a frequency of 0.5 Hz and a wavelength of 3 m?
v = f λ
f = 0.5 Hz
λ = 3 m
v = 0.5 Hz × 3 m
v = 1.5 m/s
The speed of the wave is 1.5 m/s
Question
A sound wave has a frequency of 10 kHz and a wavelength of 3.4 cm. What is its speed?
v = f λ
f = 10 kHz = 10,000 Hz
λ = 3.4 cm = \(\frac{\text{3.4}}{\text{100}}\) = 0.034 m
v = 10 000 Hz × 0.034 m
v = 340 m/s
The speed of the wave is 340 m/s.
Question
A radio wave has a frequency of 3 MHz and a speed of 300,000,000 m/s. What is its wavelength?
v = f λ
v = 300,000,000 m/s
f = 3 MHz = 3 x 106 Hz
300,000,000 m/s = 3 x 106 Hz x λ
λ = \(\frac{\text{300,000,000}}{\text{3 x 10}^6}\)
λ = 100 m
The wavelength of the radio wave is 100 m.
Frequency and time period equation
The frequency of a wave can also be calculated using this equation:
\(\text{frequency =}~\frac{\text{1}}{\text{time period}} \)
\(\text{f =}~\frac{\text{1}}{\text{T}}\)
where:
f = frequency = number of waves produced by a source per second, in hertz Hz.
T = period = time it takes for one complete vibration or oscillation, in seconds s.
Example
A sound wave has a time period of 0.0001 seconds. What is its frequency?
Answer
\(\text{f =}~\frac{\text{1}}{\text{T}}\)
\(\text{f =}~\frac{\text{1}}{\text{0.0001 s}}\)
f = 10,000 Hz
The frequency of the sound wave is 10,000 Hz.
Question
A radio wave has a frequency of 3 MHz. What is its period?
\(\text{T =}~\frac{\text{1}}{\text{f}}\)
f = 3 MHz = 3 x 106 Hz
\(\text{T =}~\frac{\text{1}}{\text{3}\times{10}^{6}{Hz}}\)
T = 0.00000033 s
T = 0.33 x 10-6 = 0.33 μs
The period of the radio wave is 0.33 μs
Question
A boat at sea bobs up and down as waves pass. The vertical distance between a crest and a trough is 52 cm and 20 waves pass the boat in 30 seconds.
- What is the amplitude of the waves?
- What is the frequency of the waves?
- The amplitude of a wave is the maximum displacement of a point of a wave from its rest position. This is exactly half the distance between a crest and trough.
The distance between a crest and trough = 52 cm.
\(\text{amplitude =}~\frac{\text{distance between a crest and trough}}{\text{2}}\) = \(\frac{\text{52 cm}}{\text{2}}\) = 26 cm.
The amplitude of the wave is 26 cm.
- \(\text{frequency f =}~\frac{\text{number of waves to pass a point}}{\text{time taken in seconds}}\)
number of waves = 20
time taken = 30 s
\(\text{f =}~\frac{\text{20}}{\text{30}}\)
f = 0.67 Hz
The frequency of the waves is 0.67 Hz.
Question
A tuning fork has a frequency of 440 Hz.
- What does a frequency of 440 Hz mean?
- Calculate the period of vibration.
A frequency of 440 Hz means that the prongs of the tuning fork vibrate 440 times every second.
\(\text{period T =}~\frac{\text{1}}{\text{f}}\)
\(\text{period T =}~\frac{\text{1}}{\text{440 Hz}}\)
T = 0.0023 s = 2.3 x 10-3 s or 2.3 ms.
The period of vibration is 0.0023 s.
Key point
There are three equations for calculating frequency:
\(\text{frequency f =}~\frac{\text{number of waves to pass a point}}{\text{time taken in seconds}}\)
\(\text{f =}~\frac{\text{v}}{\text{λ}}\)
\(\text{f =}~\frac{\text{1}}{\text{T}}\)
Use the information given in the question to select the appropriate equation to use.
How much do you know about the features of waves?
More on Unit 2: Waves
Find out more by working through a topic
- count3 of 5
- count4 of 5
- count5 of 5

- count1 of 5
