Key points
Squares, cubes and higher powers are shown as small digits called indicesIndices are powers eg, 3 to the power of 2, written 3² (sometimes these are called powersHow many times to use the number in a multiplication. For example, 3² is 3 to the power of 2 or 3 squared. or exponentThe exponent of a number says how many times to use the number in a multiplication. Also known as index, a number, positioned above and to the right of another (the base), indicating repeated multiplication when the exponent is a positive integer.). Indices is the plural of indexPositioned above and to the right of a number. It is an abbreviation of repeated multiplication. Eg, 7³ means 7 x 7 x 7.
Laws of indices provide us with rules for simplifying calculations or expressions involving powers that have the same baseThe number that gets multiplied when using an exponent (index).. This means that the larger number or letter must be the same.
The opposite of squareThe square of a number is the product of the number and itself. n2 is n squared or n to the power of two. For example, the square of 2 is 2² = 2 × 2 = 4 is square rootA square root of a number is a value that, when multiplied by itself, gives the number. Eg, 4 × 4 = 16, so the square root of 16 is 4.
The opposite of cubeThe result of multiplying to power of three, n3 is n cubed or n to the power of three. For example, the cube of 2 is 2³ = 2 × 2 × 2 = 8 is cube rootThe cube root of a number is a special value that, when used in a multiplication three times, gives that number. Eg, 3 × 3 × 3 = 27, so the cube root of 27 is 3.
Index laws for multiplication
- When multiplying indicesIndices are powers eg, 3 to the power of 2, written 3² it’s important to understand index notation. For example, 7 × 7 × 7 × 7 can be recorded as 7⁴
- The index lawsIndex laws are the rules for simplifying expressions involving powers of the same base number. for multiplication only works if the baseThe number that gets multiplied when using an exponent (index). numbers are the same. Eg, in the calculation 2² x 2³ the base numbers are the same (2).
- When multiplying indices, if the base values are the same, the expression can be simplified by adding the indices.
- The index law for multiplying still applies even when indices are negative.
Examples

Image caption, Using index notation, simplify 7² x 7³

Image caption, Writing the calculation in full can help to understand how the law of multiplication works. 7 squared is 7 x 7 and 7 cubed is 7 x 7 x 7. This means that 7² x 7³ = (7 x 7) x (7 x 7 x 7)

Image caption, Multiply the powers. If the base numbers are the same (7) then add the indices together (2 + 3 = 5). 7² x 7³ = 7⁵

Image caption, Using index notation, simplify 9³ x 9⁵

Image caption, Writing the calculation in full can help to understand how the law of multiplication works. 9 cubed is 9 x 9 x 9 and 9 to the power of 5 is 9 x 9 x 9 x 9 x 9. The base numbers are the same (9), so add the indices together (3 + 5 = 8). 9³ x 9⁵ = 9⁸
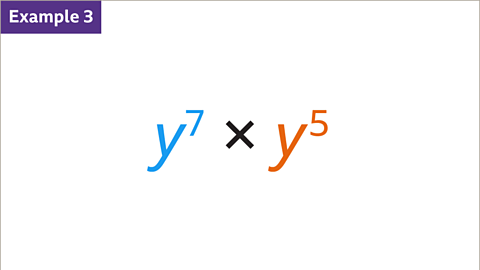
Image caption, Using index notation, simplify y⁷ x y⁵
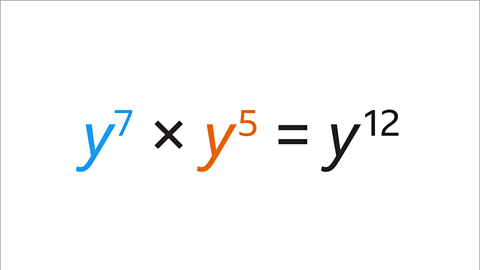
Image caption, The base values are the same (y). The rules apply whether the base is a number or a symbol. Add the indices together (7 + 5 = 12). y⁷ x y⁵ = y¹²
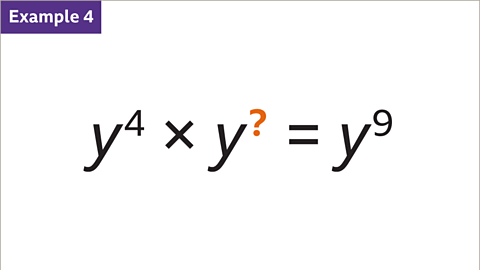
Image caption, Work out the value of the missing index value (?)
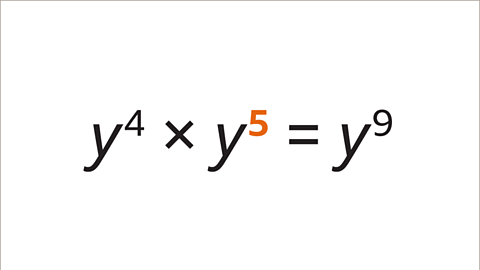
Image caption, The base values are the same (y). The two indices must add together to make 9. Working backwards 9 – 4 = 5, therefore 4 + 5 = 9. The value of the missing index value is 5. y⁴ x y⁵ = y⁹
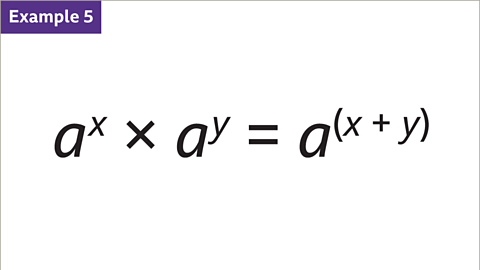
Image caption, When multiplying indices, if the base values are the same, add the indices together. aˣ x aʸ = a⁽ˣ⁺ʸ⁾. The base in this example are unknown, but they both have the same value of ‘a’.
1 of 10
Question
Find the value of the missing index value.
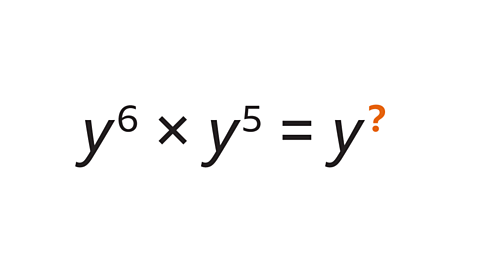

The base values are the same (y).
Add the indices together (6 + 5 = 11)
y⁶ x y⁵ = y¹¹
The missing index value is 11
Index laws for division
- When dividing indicesIndices are powers eg, 3 to the power of 2, written 3² , it’s important to understand index notation. For example, a × a × a × a × a can be recorded as a⁵
- The index lawsIndex laws are the rules for simplifying expressions involving powers of the same base number. for division only works if the baseThe number that gets multiplied when using an exponent (index). numbers are the same.
- When dividing indices, if the base values are the same, the expression can be simplified by subtracting the indices.
- Remember that division can be written as a fraction, for example 7 ÷ 2 can be written as \( \frac{7}{2} \)
Examples
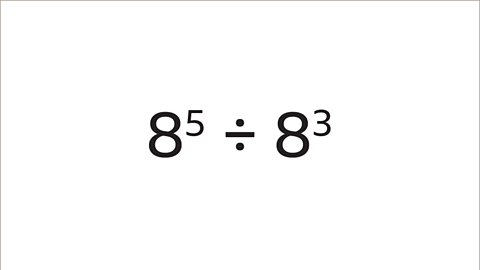
Image caption, Using index notation, simplify 8⁵ ÷ 8³
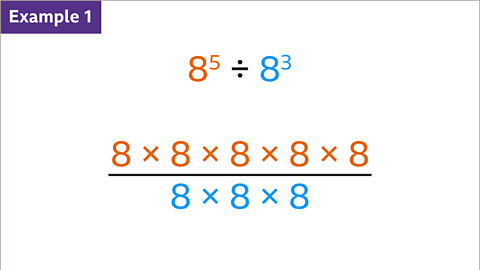
Image caption, 8 to the power of 5 is 8 x 8 x 8 x 8 x 8. 8 to the power of 3 is 8 x 8 x 8. The division can be written using a divisor (like a fraction). Writing the calculation in full can help understanding of why the law for division works.
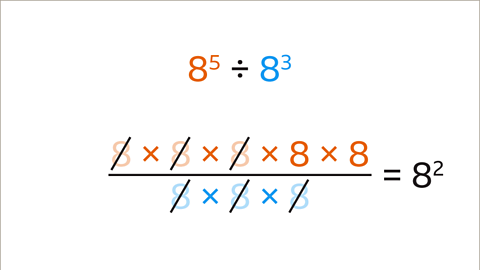
Image caption, There are common factors of 8 in the numerator and denominator. These can be cancelled out. Cancelling 8 from both the numerator and denominator simplifies the fraction. We can do this three times. Of the five 8s in the numerator, three can be cancelled with the 8s in the denominator. This leaves 8 x 8 = 8²
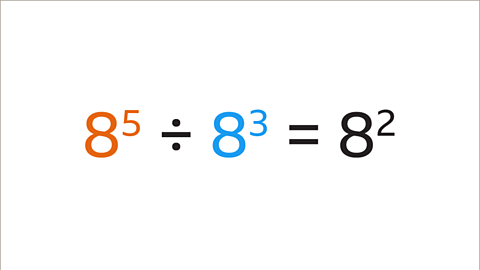
Image caption, When dividing powers, if the base numbers are the same (8), subtract the indices to simplify. (5 - 3 = 2). 8⁵ ÷ 8³ can be simplified to 8²

Image caption, Using index notation, simplify t⁶ ÷ t²
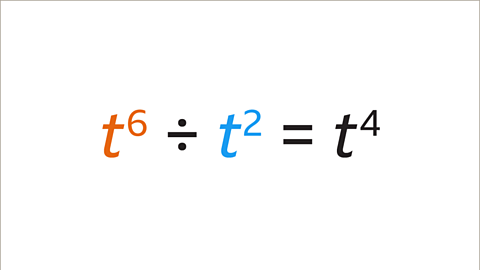
Image caption, The base values are the same (t). The rules apply whether the base is a number or a symbol. Subtract the indices (6 - 2= 4). t⁶ ÷ t² = t⁴

Image caption, Work out the value of the missing index value.
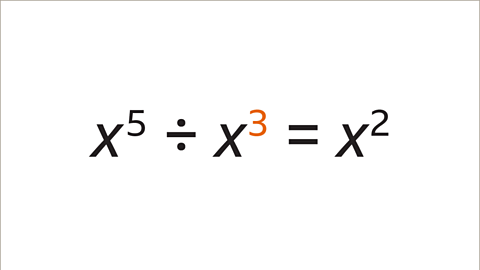
Image caption, The base values are the same (x). Subtracting the two indices must make 2. Starting at 5, work out what needs to be added/subtracted in order to get to 2 (subtract 3). x⁵ ÷ x³ = x²
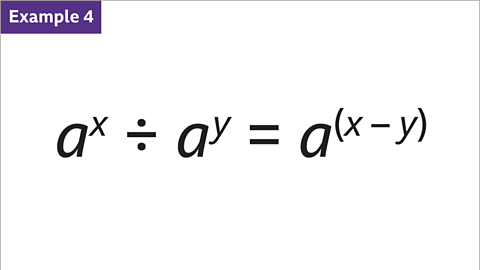
Image caption, When dividing indices, if the base numbers are the same, subtract the indices. aˣ ÷ aʸ = a⁽ˣ⁻ʸ⁾. The base in this example is unknown, but they both have the same value of ‘a’.
1 of 9
Question
Work out the value of the missing index value.

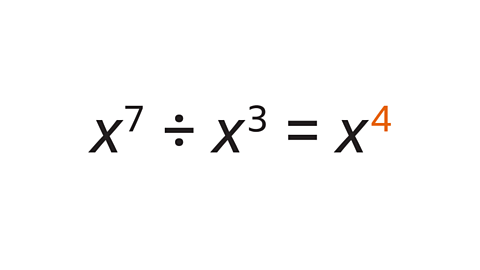
The base values are the same (x).
Subtract the indices (7 – 3 = 4)
x⁷ ÷ x³ = x⁴
The missing index value is 4
Practise laws of indices
Practise what you have learned about the laws of indices with this quiz.
Quiz
Game - Divided Islands
Play the Divided Islands game! gamePlay the Divided Islands game!
Using your maths skills, help to build bridges and bring light back to the islands in this free game from BBC Bitesize.
